Houston, TX |
In this E-Tip, the second in our Compression Basics series, we will explore some basic gas properties to see how gases respond to changes in pressure and temperature and what that means for the amount of gas that can fit in our compressor at suction conditions.
Natural Gas
Natural gas is the result of decomposed organic matter and is a mixture of hydrocarbon gases and various impurities. It is composed of light weight hydrocarbon elements ranging from methane (CH4) to octane (C8H18). In addition to these hydrocarbon elements, natural gas can also contain various amounts of carbon dioxide (CO2), Nitrogen (N2), hydrogen sulphide (H2S) or Helium (He).
Before trying to understand gas compressor design and operation, it is important to first have a working knowledge of basic gas behaviour. All gases behave essentially the same with respect to changes in pressure, temperature and volume. These relationships between pressure, temperature and volume are known as the fundamental laws of gas behaviour. However, before we examine these Gas Laws, there are a few concepts that are important to understand.
Atmospheric Pressure
The pressure exerted by the gases on the earth’s surface is known as atmospheric pressure. At sea level, the pressure is 101.3 kilopascals (kPa) or 14.7 pounds per square inch (PSI). At elevations above sea level, the pressure exerted by the earth’s atmosphere becomes less because air is less dense as the elevation increases.
Gauge Pressure
This is the pressure indicated on a pressure gauge and is expressed as the pressure above, but not including, atmospheric pressure. It is normally indicated in kPag or PSIG.
Absolute Pressure
Gauge pressure plus atmospheric pressure is Absolute Pressure and it is abbreviated kPaa.
Example: 20 kPag (gauge pressure) is equivalent to 121.6 kPaa (absolute pressure) at sea level and 111.92 kPaa at 1000 meters elevation above sea level.
Absolute Temperature
Absolute zero is the temperature at which all molecular motion ceases – minus 273.15°C. The unit for absolute temperature is Kelvin (K) and is the reading of the thermometer in degrees Celsius plus 273.15°C.
Example: A thermometer reading 80°C equals as absolute temperature of 80 + 273.15 or 353.15K.
Absolute Pressure and Temperature
All compressor calculations are performed in absolute units of pressure and temperature.
Basic Gas Laws
In compression, we are interested in the relationship between Volume, Pressure, and Temperature of natural gas and we can use Thermodynamics to understand these relationships. These principles are called the Gas Laws.
Boyle’s Law
During the seventeenth century, Robert Boyle observed that if the temperature of a gas remains constant, its volume varies inversely with the absolute pressure. In other words, reducing volume increased the pressure.
Boyle’s Law:
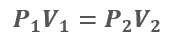
Charles’ Law
Nearly one hundred years after Robert Boyle discovered the relation between gas pressure and gas volume, Jacques Charles discovered that if pressure remains constant, the volume of a gas increases proportionately with any increase in temperature. Therefore, as the temperature of gas increases, the volume increases if pressure remains the same.
Charles’ Law: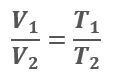
Combined Gas Law
Boyle’s and Charles’ laws can be combined to form the combined gas law. This fundamental law is one of the most widely used relations in gas measurement work. It approximates the behavior of many gases under conditions close to ordinary atmospheric temperatures and pressures. At low pressures, most gases behave like an ideal gas and follow the ideal gas laws quite closely.
Combined Gas Law: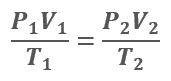
Compressibility Factor
When gas pressure increases, a wide variation between ideal and actual gas behavior may occur. The deviation of a gas from the ideal gas laws is known as the compressibility factor and is commonly designated with the symbol ‘Z’. Compressibility is a function of temperature, pressure and the nature of the gas, and is experimentally derived from data of the actual behavior of a particular gas under pressure, volume and temperature changes. The ‘Z’ factor is used as a multiplier to adjust the ideal gas law to fit actual gas behavior.
Gas Constant and Moles
Avogadro’s law states that “equal volumes of all gases, at the same temperature and pressure, have the same number of molecules". It provides the basis to calculate the number of constituent particles of gas in a sample. Multiplied by the Boltzmann constant, Avogadro’s Number becomes the Universal Gas Constant, R. When combined with the Basic Gas Law, the gas constant allows us to calculate how much gas, or how many moles of gas, exist in a volume.
Ideal Gas Law
Shown below is the Ideal Gas Law with Compressibility and the Universal Gas Constant, which can be used to quantify the number of molecules of a known gas composition that can fit into a defined volume, VS, under known conditions, PS and TS.
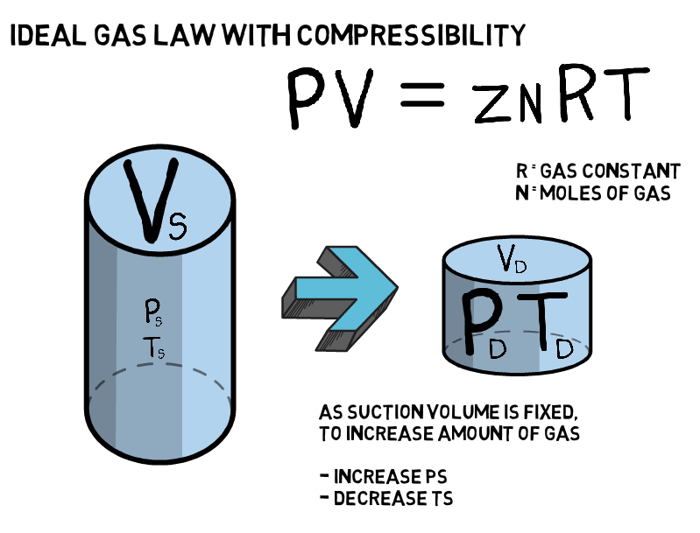
Gas Laws and Compression
If, for now, we imagine a compressor to be a known fixed volume, such as Vs in the image above, we can use the underlying fundamentals of the ideal gas law to explain some key features of a compressor performance curve.
As the compressibility factor, Z, is essentially constant for permissible compressor suction conditions, R is constant and Vs is fixed, we can simplify the ideal gas law above to:
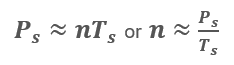
The above equations tell us that the amount of gas, n, is proportional to the suction pressure, Ps, and inverse of the suction temperature, Ts.
Suction Pressure
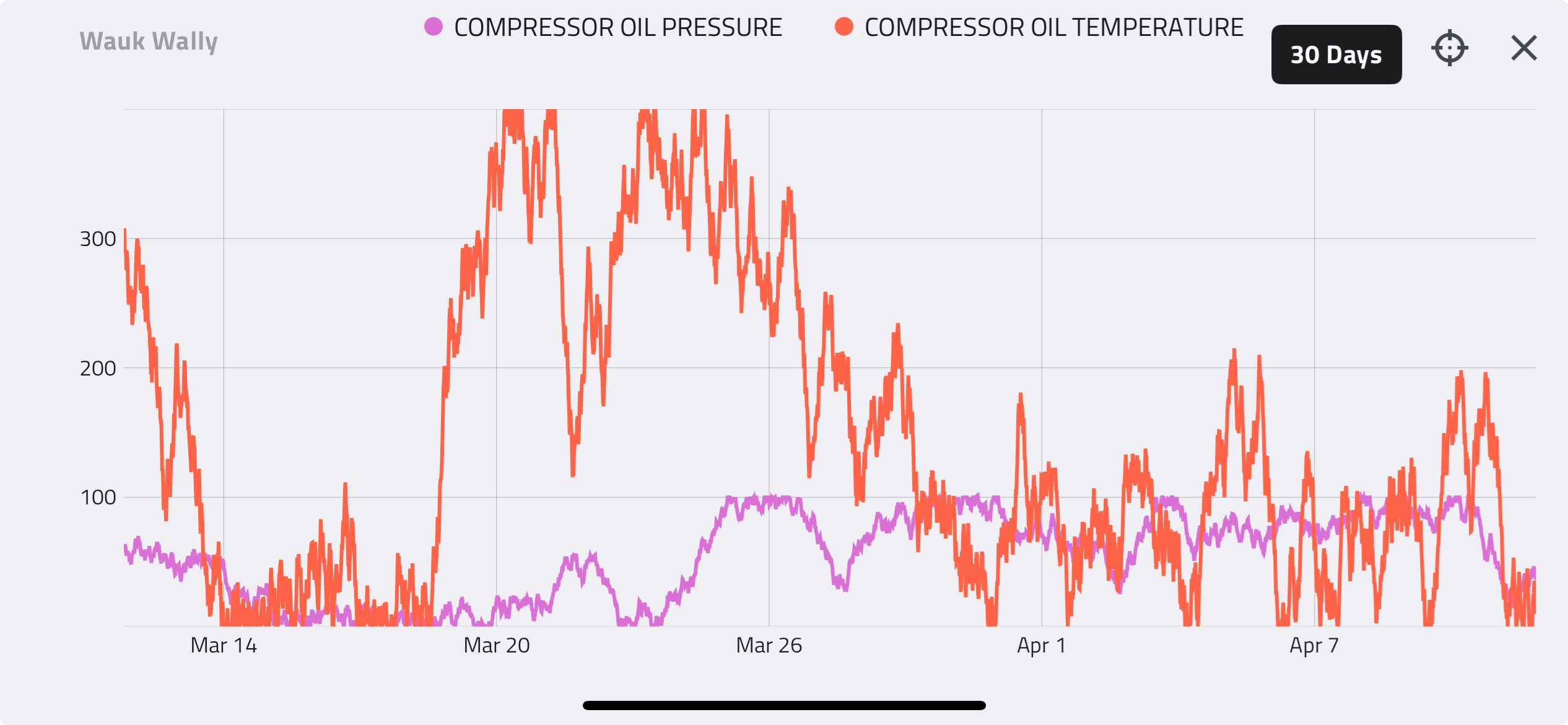
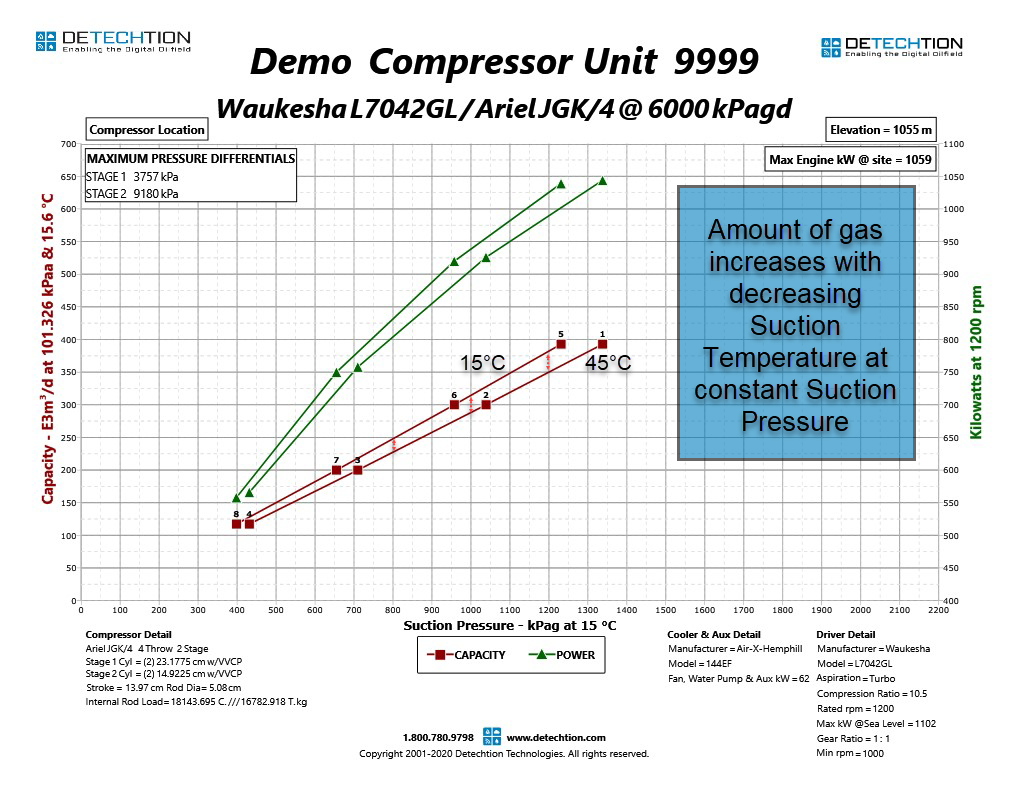
Again, assuming a compressor can be approximated by a fixed volume, the relationship above shows that the only way to put more gas into the compressor is by doing so at a higher pressure, assuming temperature remains constant. We can see this relationship clearly in the compressor performance curve below.
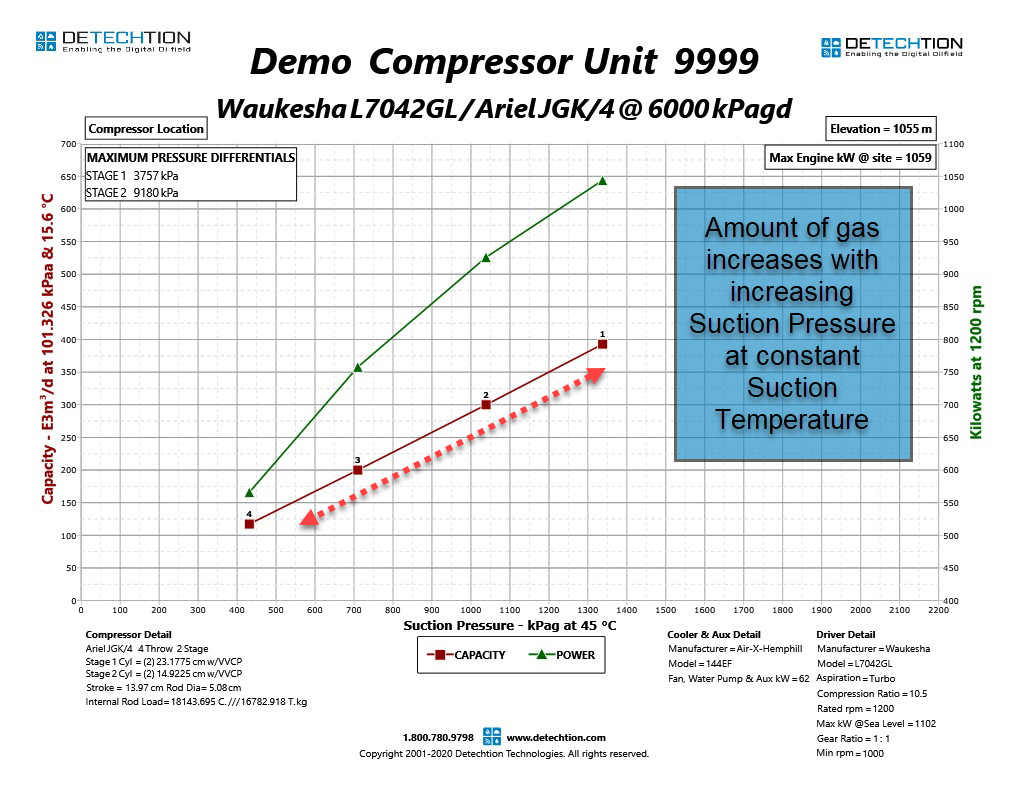
The fundamental gas laws explain why compressor capacity increases with increasing suction pressure. In reality, this relationship is not perfectly linear. This will be explained in more detail later in this Compression Basics E-Tips series.
Suction Temperature
Similarly, we can show how the gas laws apply to varying suction temperatures. The gas laws show that the number of moles of gas in a fixed volume will increase with decreasing temperature. The performance curve below shows compressor capacity at 45°C and 15°C. At any given suction pressure, the capacity of the compressor is greater when the suction temperature is 15°C than at 45°C. This means that more molecules of gas fit into the same volume at lower suction temperatures.
In the next E-Tip in this series, we will look at the role compression plays in natural gas production. Click here to read E-Tip 1.18 now!
For more E-Tips, please visit the Detechtion Technologies Learning Center.